自动驾驶感知融合(2):无迹卡尔曼滤波(Lidar&Radar)

Unscented Kalman Filter
Overview
我们简单回顾下KF及EKF滤波:
卡尔曼滤波器: 假设数据为高斯分布形式,我们将线性方程式应用于该高斯分布的数据,然后使用一系列卡尔曼滤波公式获得最优状态预估。
扩展卡尔曼滤波:然而现实世界并不是线性的,当传感器在一个方向上进行测量时,我们可能会在另一个方向上进行预测,这样会涉及非线性的角度和正弦余弦函数。因此,EKF可以借助泰勒级数(以及雅可比矩阵)在高斯均值附近线性近似非线性函数,然后预测其值。
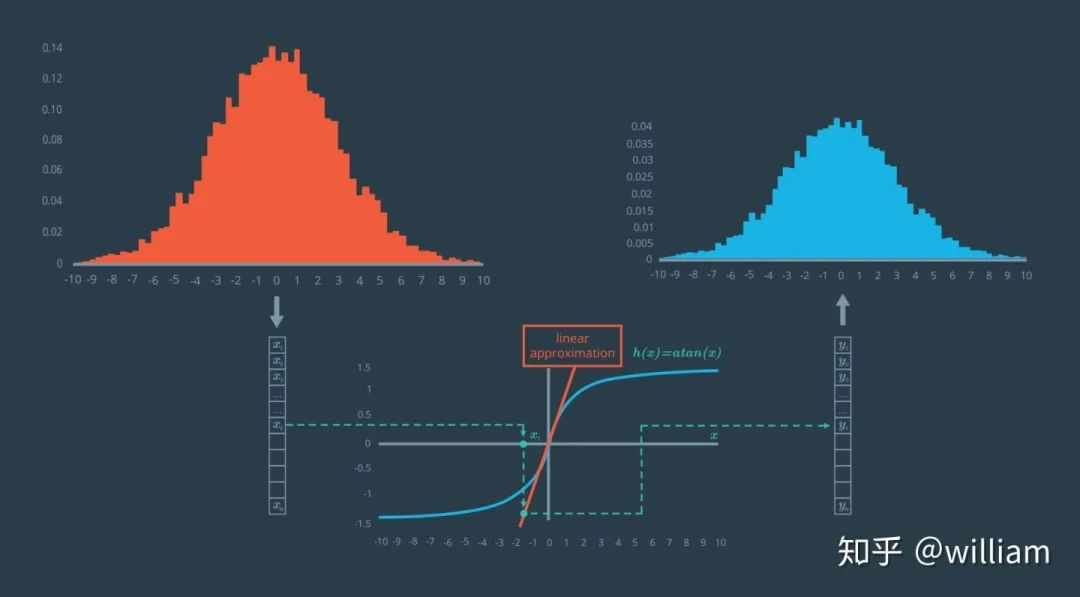
1. 既然EKF已经能够很好的解决非线性问题了,为什么还需要UKF?
原因是现实生活中存在很多完全不规律的分布,我们需要更好的近似方式和更高的性能。
让我们来看下在EKF中如何解决非线性问题的:
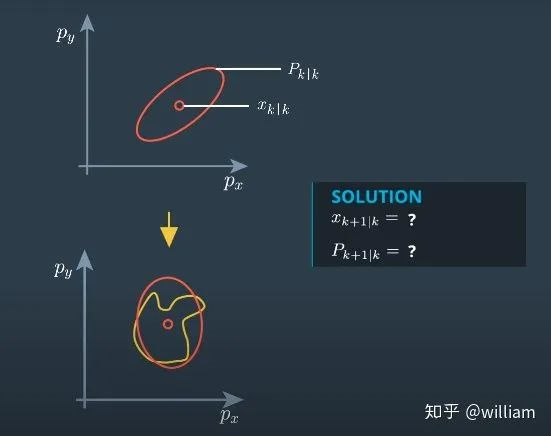
可以看到原始高斯分布经过非线性变换之后其实是一个不规则的非线性分布,在EKF中我们在高斯均值点附近用泰勒级数近似非线性分布,从而获得近似高斯分布。但是问题在于,这个近似高斯分布有时不是足够精确,单单一个均值点往往无法预测上图中这种很不规则的分布的。这个时候我们就需要无迹卡尔曼滤波UKF了。
值得注意的是尽管Unscented Kalman Filter通常被叫做无迹卡尔曼滤波,但是在有的文献中存在另外一种叫法:无损卡尔曼滤波,这两种叫法都是可行的。
2. UKF是怎么解决复杂不规则分布的?
UKF从原始高斯分布中提取包括均值点在内的一系列代表点,并将代表点带入到非线性等式中,围绕这些点进行近似,从而获得更好的近似结果。
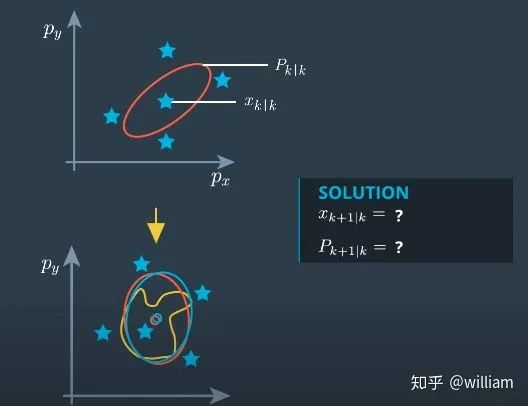 在上图中我们可以看到,蓝色椭圆代表的UKF近似高斯分布更接近真实的不规则分布。
在上图中我们可以看到,蓝色椭圆代表的UKF近似高斯分布更接近真实的不规则分布。
总的来说,与EKF相比,UKF是处理非线性过程模型或非线性测量模型的更好的替代方法。UKF不会对非线性函数进行线性化处理,它用所谓的sigma 点来近似概率分布。其优势在于在很多情况下,sigma 点近似非线性转换的效果比线性化更好,此外它还可以省去计算复杂的雅可比矩阵的过程
3. UKF 代表点的数量是不是越多越好?
从原始高斯分布中提取的点的数目越多,我们的近似就越精确,但是相应计算资源的消耗就越大。将原始高斯分布中所有的数据点进行非线性变换和近似处理是最简单的解决方案,但不是最佳方案。
4. 如何选择合适的UKF代表点?
UKF代表点被称为sigma 点,它们分布在状态均值的周围,并且和每个状态维度的标准偏差信号(即σ)有关,因此被叫做sigma 点。它们代表了整个分布。在这里值得注意的,我们可能会根据实际需求或多或少优先考虑某些点,从而使我们的近似性更好,这就需要为每一个sigma 点赋予权重。如何合理选择sigma 点的个数,并且为不同的sigma 点赋予权重是UKF应用的重点,我会在接下来的章节详细描述。
由于无迹卡尔曼滤波是在卡尔曼滤波的基础上开发的,在本文中对于一些基础概念我并没有详细解释,如果有什么疑问,请参看我的上一篇文章“卡尔曼及扩展卡尔曼滤波(Lidar&Radar)”。
Unscented Transform
当高斯分布经过非线性函数变换后,它不再是高斯分布,而无迹卡尔曼滤波通过无迹转换将非线性函数变换的结果近似成高斯分布。
以下是无迹变换执行的步骤:
1.计算Sigma点集
2.为每个Sigma点分配权重
3.把所有单个Sigma点代入非线性函数f
4.对经过上述加权和转换的点近似新的高斯分布
5.计算新高斯分布的均值和方差。
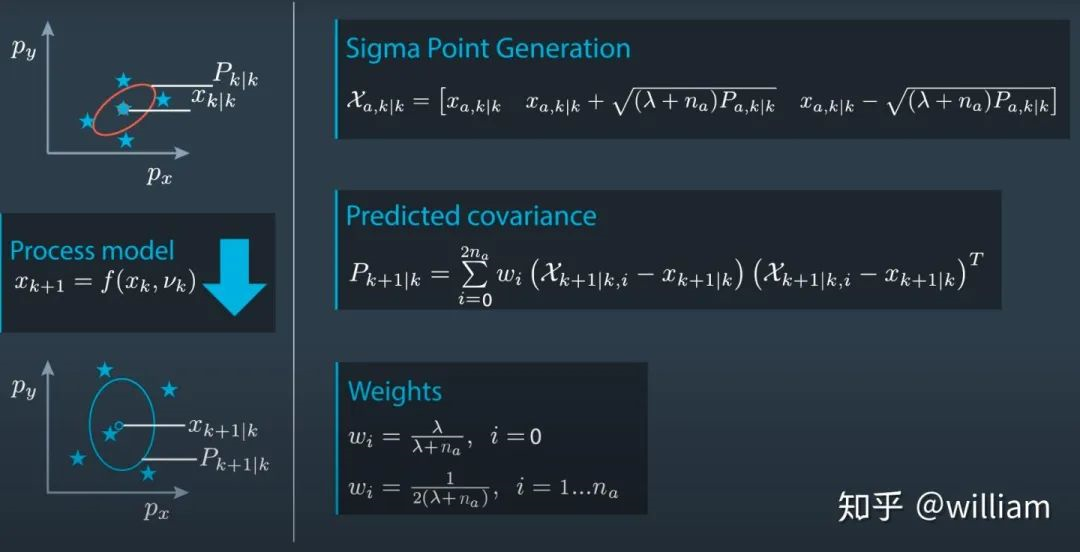
计算Sigma 点集
选择合适的sigma 点数量n取决于系统的状态维度N:n=2N+1。
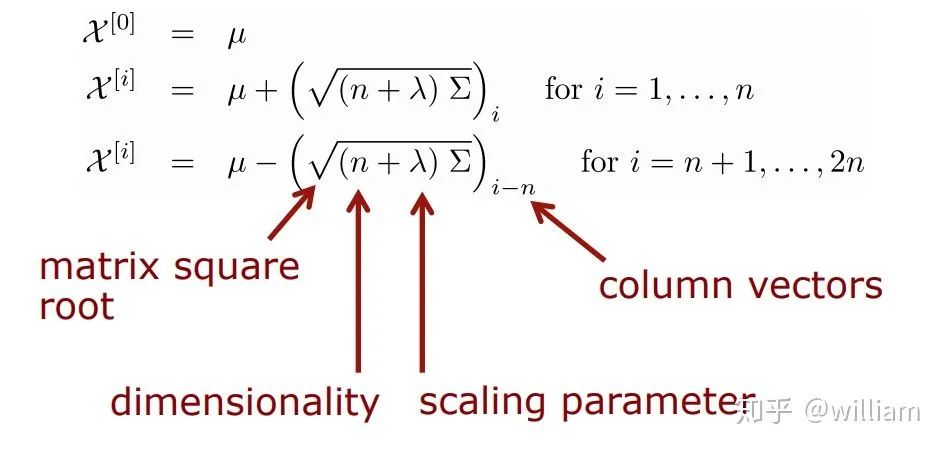
公式1
我们可以根据公式1计算sigma 点 矩阵,值得注意的是到第1个点和其之后的点有不同的计算公式,这是由于第1个点是均值点,其余点都是围绕均值的sigma 点。
以下是公式1中部分参数的含义:
χ表示 sigma 点矩阵。矩阵中每一列都表示一组sigma 点。如果系统是2维空间,那么矩阵的大小将是2 x 5。每个维度有n=2N+1=5个sigma 点。可以看到,同一列的sigma 点有两个对称的计算公式,这是由于同一列的上下两个sigma 点在原始高斯分布中围绕均值点呈对称分布。
λ是比例因子,它告诉我们应该选择距离均值多远的sigma 点。数学研究表明,λ的最佳值为3-n。
Σ被称为协方差矩阵,对Σ求平方需要找到一个满足以下条件的矩阵 S: Σ = S.S or Σ = S.S_transpose,S= √∑。
计算sigma点的权重
在我们挑选出合适的sigma 点之后,我们需要为每个sigma 点赋予合适的权重:
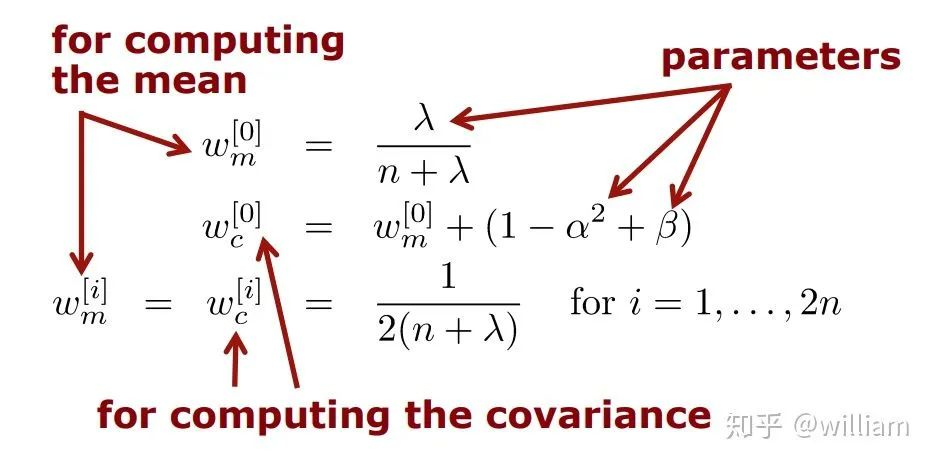
公式2
值得注意的是计算均值权重的公式与计算其余sigma 点权重的公式也是不同的,而且所有代表点权重之和等于1。
无迹转换参数
sigma 点的选择和权重计算公式主要有以下四个可调节参数,这些参数被称作UT Parameters, 我们可以使用这些参数对无迹变换进行缩放:

其中最重要的是 λ 扩散参数,数学研究表明,λ的最佳值为3-n。如果λ已经给出,其余UT参数可以考虑省略,从而简化公式,如在有的资料中计算sigma 点权重的公式为
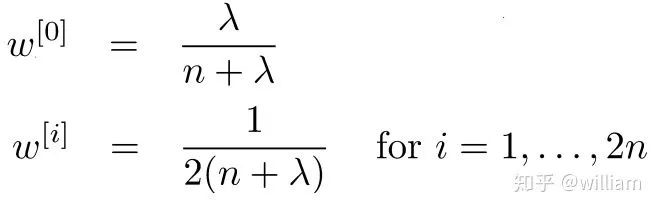
如在这个公式中没有ωc和ωm。
本项目中使用简化的sigma 点权重计算公式。
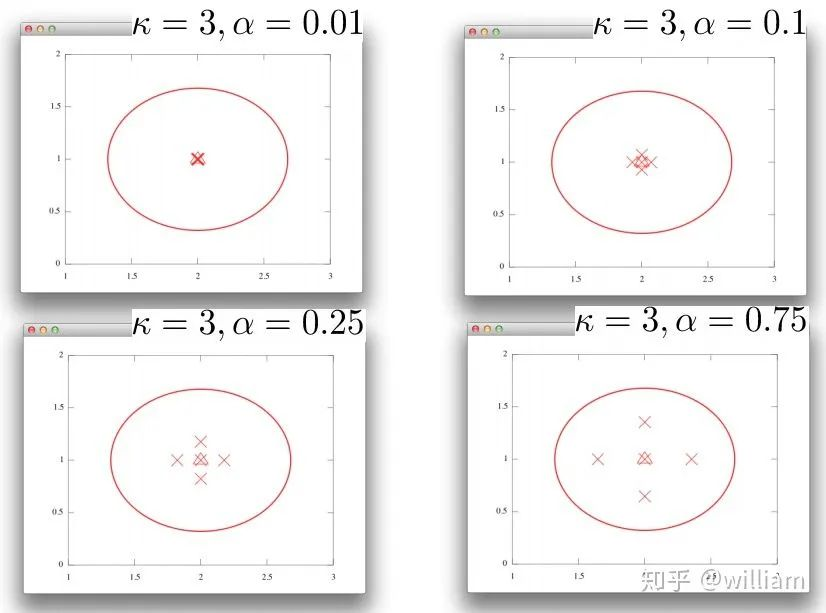
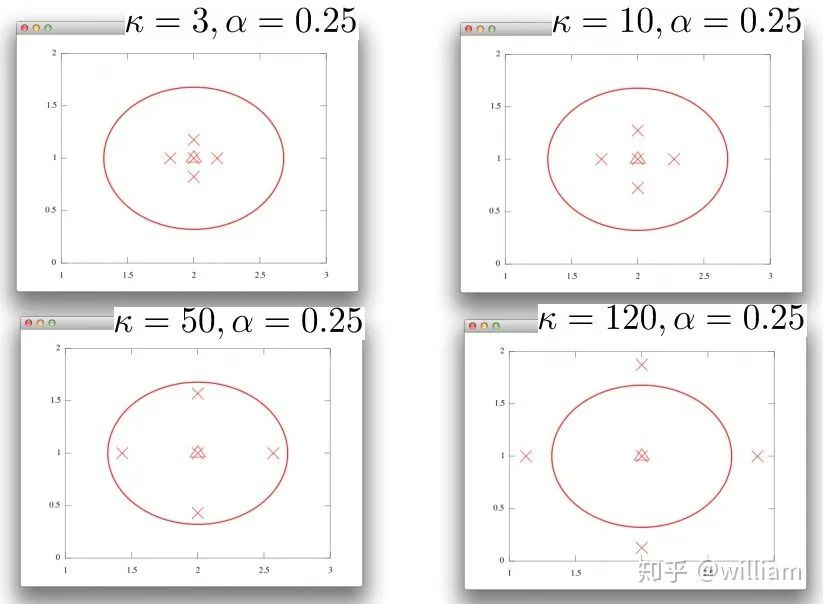
但是理解 λ 扩散参数的原理是很有必要的, λ 扩散参数由k,α,n三个参数计算得到,下图是不同k和α的组合对于sigma 点分布的影响。
计算近似高斯分布的均值和协方差
现在我们已经得到了带有权重的,经过非线性等式转换后的sigma 点,我们可以通过这些sigma 点近似新的高斯分布,并计算其均值及协方差。
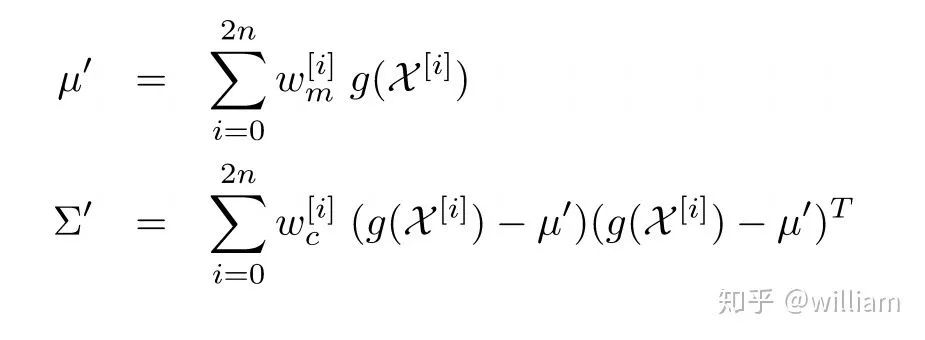
公式3
下面是公式3中各个参数的含义:
μ′ -> Predicted Mean Σ′ -> Predicted Covariance w -> Weights of sigmas g -> Non Linear function χ(Caligraphic X) -> Sigmas Matrix n -> Dimentionality
这样我们就完成了无迹变换的全部过程,现在让我在预测更新和测量更新中融入无迹卡尔曼滤波。
UKF Roadmap
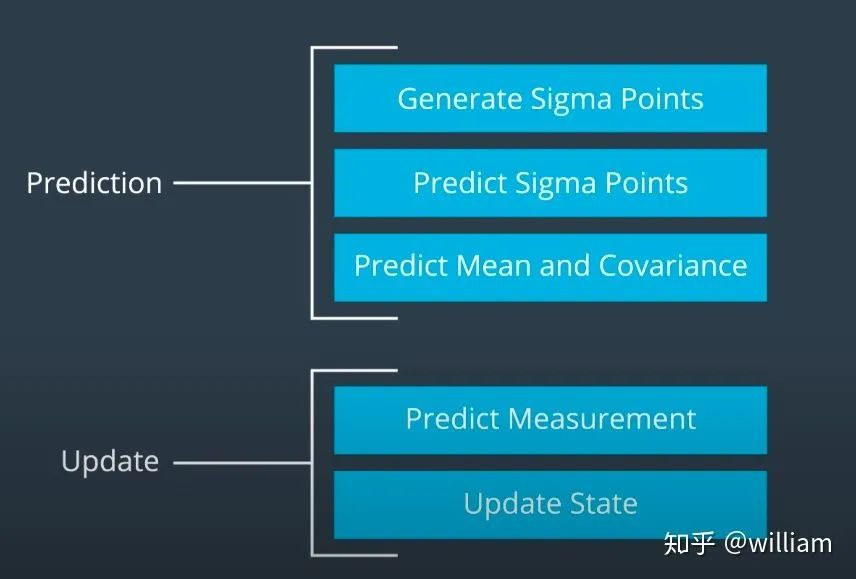
Prediction
预测步骤基本上与我们上文中讨论到的无迹变换非常接近
使用公式1计算Sigma 点。
使用公式2计算Sigma点的权重。
使用公式3转换Sigma 点并计算新的均值和协方差。由于此时我们的不确定性增加了一些,因此我们必须考虑添加过程噪声R。
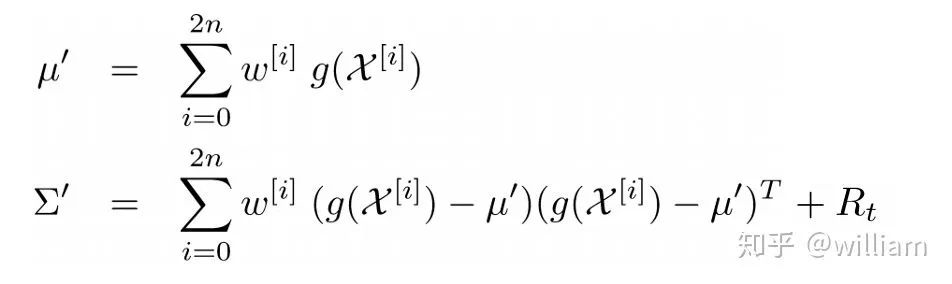
公式4
Measurement
在预测更新后我们得到了预测值的均值和协方差。当我们得到来自传感器的测量值后,如果我们想获得预测值和测量值之间的差值,我们得首先从预测的状态空间转换到测量状态空间。
如果状态空间的转换是非线性的,则就需要像预测步骤一样进行无迹转换。
通过公式h(x)我们可以把预测状态空间转换为测量状态空间。
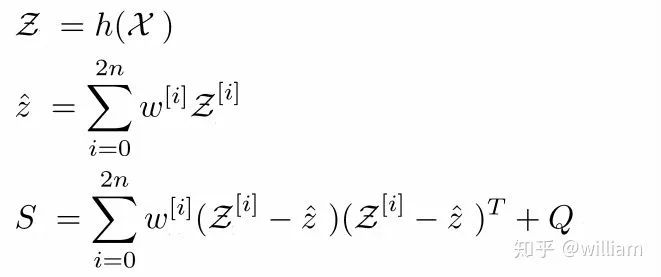
公式5
下面是公式5中各个参数的含义:
Z -> transformed sigmas in measurement space χ(Caligraphic X) -> Sigmas Matrix ẑ -> Mean in measurement space S -> Covariance in measurement space Q-> Noise h-> is a function that maps our sigmas to measurement space
这里需要注意,由于我们不再将函数线性化,因此我们不再有雅可比行列式。
接下来我们需要计算卡尔曼增益k:
首先我们要计算预测误差:状态空间中的sigma点与测量空间中的sigma点之间的交叉关联矩阵T。
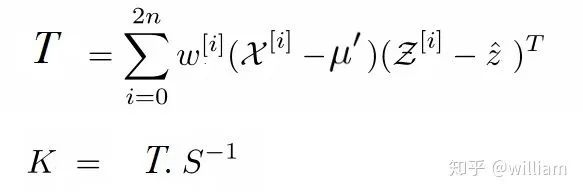
公式6
下面是公式6中各个参数的含义:
T -> Cross Co-relation Matrix between state space and predicted space S-> Predicted Covariance Matrix K-> Kalman Gain
虽然EKF和UKF计算卡尔曼增益k的公式是看起来不同,但其实很相似:
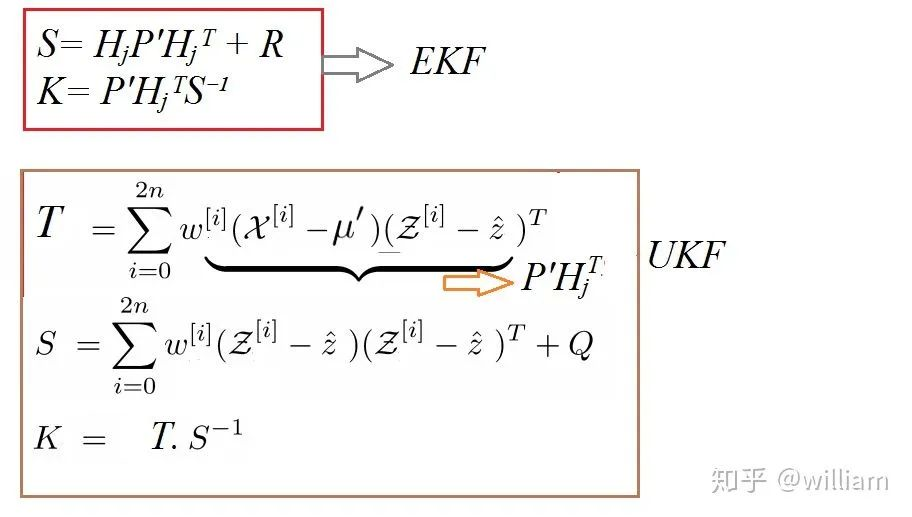
公式7
而最终在测量状态中更新预测值的等式则是相同的。
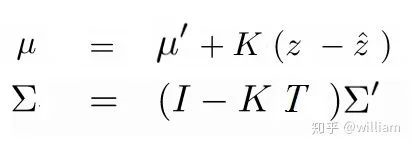
公式8
下面是公式7, 8中各个参数的含义:
μ -> Mean Σ -> Covariance μ′ -> Predicted Mean Σ′ -> Predicted Covariance K -> Kalman Gain z-> Actual Measurement Mean coming from the sensor ẑ -> Mean in measurement space T -> It is the same as H in Kalman Filter and Hⱼ in EKF. Here it is cross co-relation matrix
EKF VS UKF
我们已经介绍完无迹卡尔曼滤波了,现在来总结一下两者的区别。
对香蕉形状的近似估计是最能体现两者性能区别的实验。
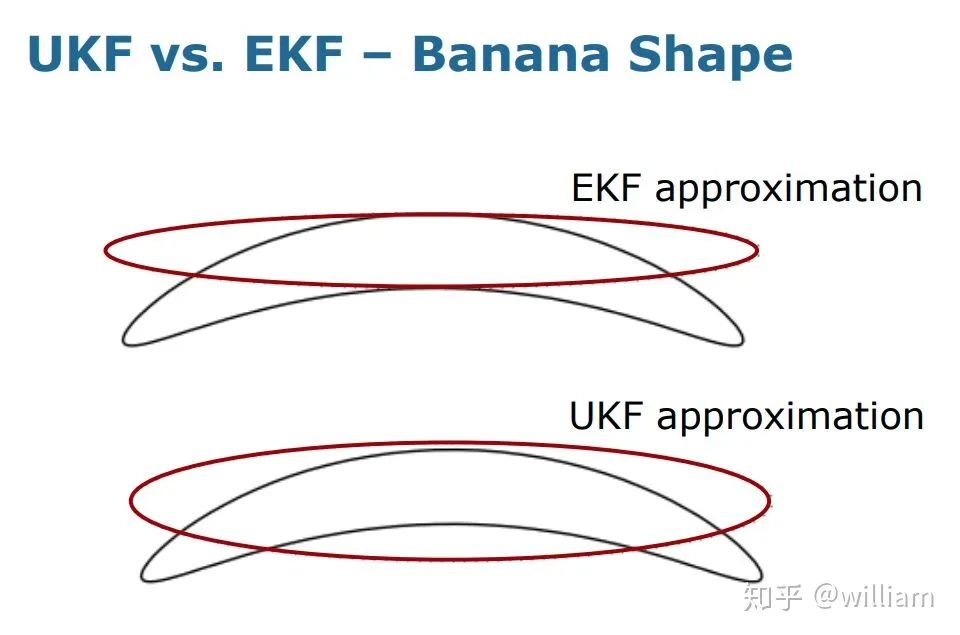
我们可以明显看到UKF近似非线性模型的优越性。
下图真实展示了EKF近似非线性模型的不足,即很有可能大范围偏离真实分布。
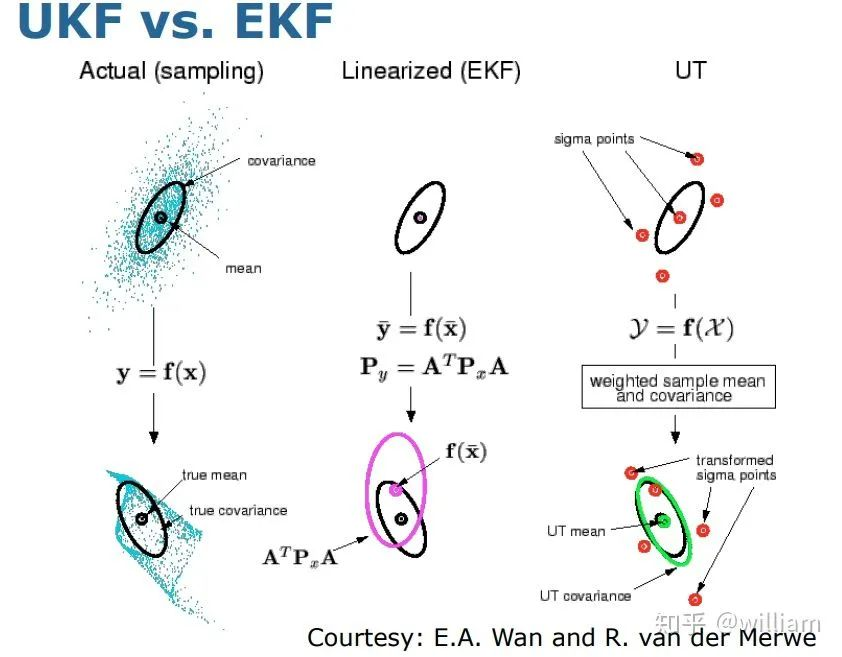
虽然UKF不需要雅可比矩阵,但是其实具有相同的复杂度等级,对于规则分布的近似甚至可能会慢一点,与EKF的效果差异有的时候很小,只是在EKF中有的时候雅可比矩阵很难推导,这也是无迹卡尔曼滤波作者开发这一算法的起因之一。
Constant turn rate and velocity magnitude model (CTRV)
在扩展卡尔曼滤波器课程中,我们使用了恒速模型(CV)。恒速运动模型是目标跟踪最基本的运动模型之一。
但是恒速模型在现实生活中存在局限性,恒速模型无法正确预测拐弯的车辆。
除了恒速模型还有许多其他模型,包括:
constant turn rate and velocity magnitude model (CTRV)
constant turn rate and acceleration (CTRA)
constant steering angle and velocity (CSAV)
constant curvature and acceleration (CCA)
Constant Heading and Constant Velocity (CHCV)
每个模型都对一个物体的运动做出不同的假设。这些模型适合真实的交通场景。
我们可以在任意一个模型上使用扩展卡尔曼滤波器或者无迹卡尔曼滤波。
在本文中,我们只讨论CTRV模型。
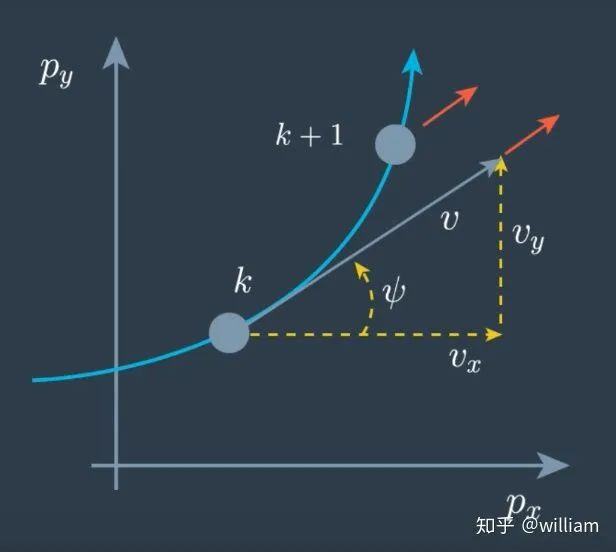
1. 首先我们来看看CTRV模型的状态向量及过程模型的定义:
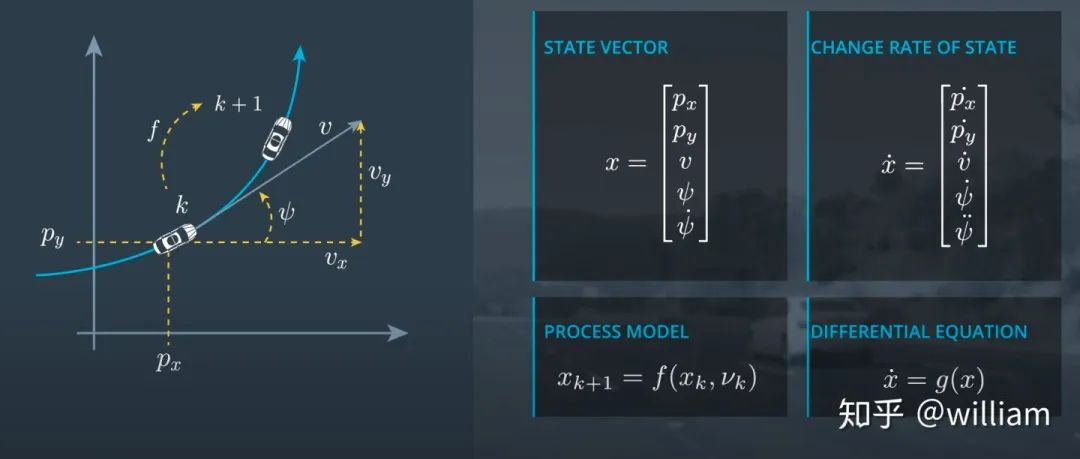
其中ψ为角度,ψ˙为角速度,ψ¨为角速度变化率。
尽管我们知道了CTRV模型的状态向量,我们需要预测时间k+1时车辆的位置,但是我们对于过程模型的推导仍然毫无头绪。这个时候我们就需要借助状态向量的变化率,通过差分方程来推演真实世界中的过程模型。
通过对状态向量求导我们得到了其差分方程:
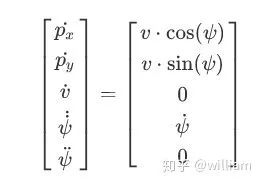
时间差:
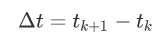
求微积分:

微积分推导的步骤相对复杂,可以使用WolframAlpha的积分工具求微积分。
微分结果:
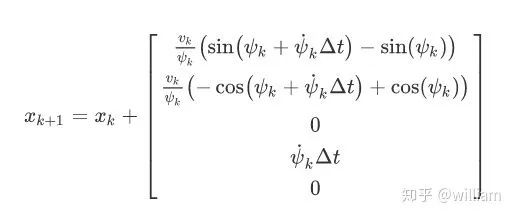
但是这个等式有一个问题:ψ˙ 不能为0,也是说这个等式不能解决车辆沿(斜)直线行驶的问题(ψ˙=0,ψ可以不等于0)。
对于ψ˙=0的情况我们可以直接求解斜三角。
即:
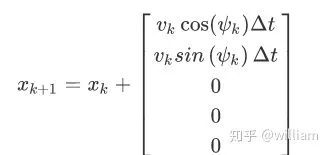
2. 在确定过程模型的固定部分之后,我们还需要考虑过程噪声项,这就涉及到过程噪声νk。
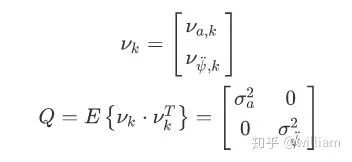
我们用一个二维噪声向量νk来描述过程模型,不确定性νk由两个独立的标量过程噪声组成。第一个过程噪声是纵向加速噪声νa,νa是随机分布的白噪声,其均值为0,方差为σa的平方,即
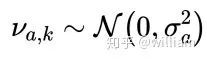
。第二个过程噪声是角加速度噪声νψ˙˙,
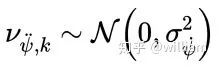
。而Q为过程噪声协方差矩阵。当我们知道噪声项之后,我们需要考虑它对整个积分方程的影响。
对于速度:
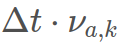
对于角度:
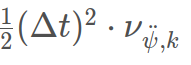
对于角速度:
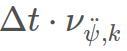
对于px和py的影响则稍微复杂点,这是由于纵向加速度和角加速度都会对位置产生影响,我们也可以用积分求得,但是如果角加速度不大的话,我们可以忽略角加速度的影响用近似求解。
px:
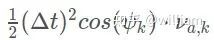
py:
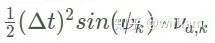
3. 在确定过程模型固定项和噪声项之后我们能得到最终的过程模型。
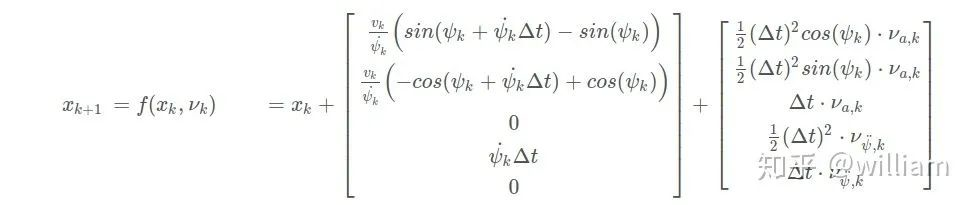
注意:此公式只适用于ψ˙不等于0的情况。
CTRV based Unscented Kalman Filter
我们已经介绍了无迹变换和CTRV模型了,现在我们来在代码中使用上述技术实现基于激光雷达和毫米波雷达的多目标追踪。
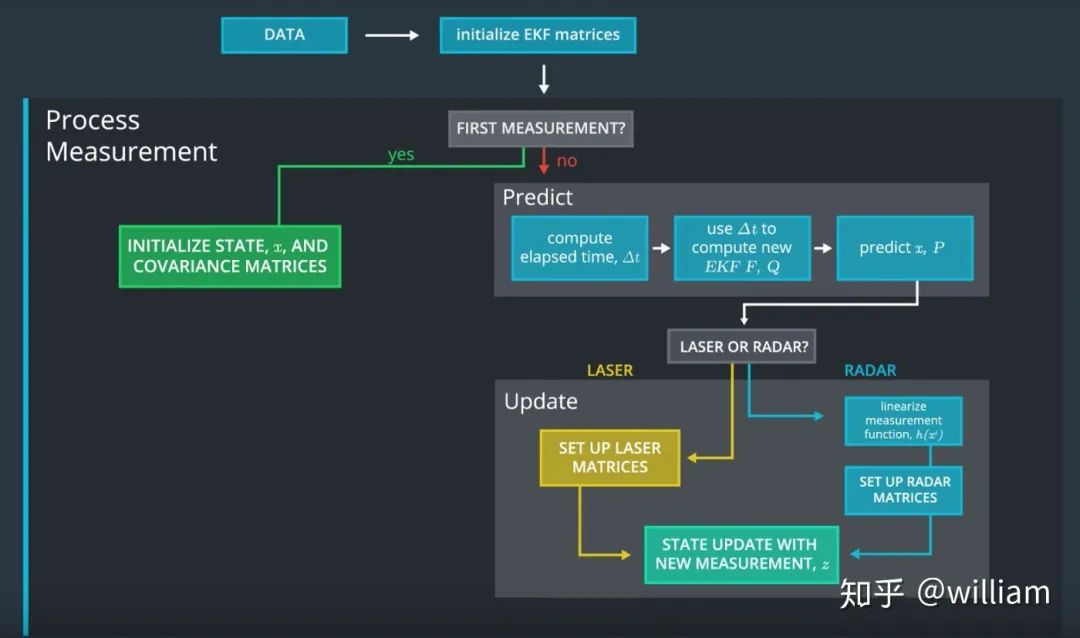
预测阶段
计算sigma点
在预测阶段的第一步,我们从先前时刻最后更新的状态和协方差矩阵中生成 sigma 点。对于 CTRV 模型,我们状态维度 N =5。但是,由于二维过程噪声向量也具有非线性效应,因此需要将二维过程噪声向量加入到新的状态向量x_aug中。其中n_aug=5+2=7. 我们将选择2n_aug+1=15个sigma 点。

预测sigma点
在第二步中,我们简单地将每个 sigma 点插入到 CTRV 的过程模型中,得到预测后的 sigma 点。
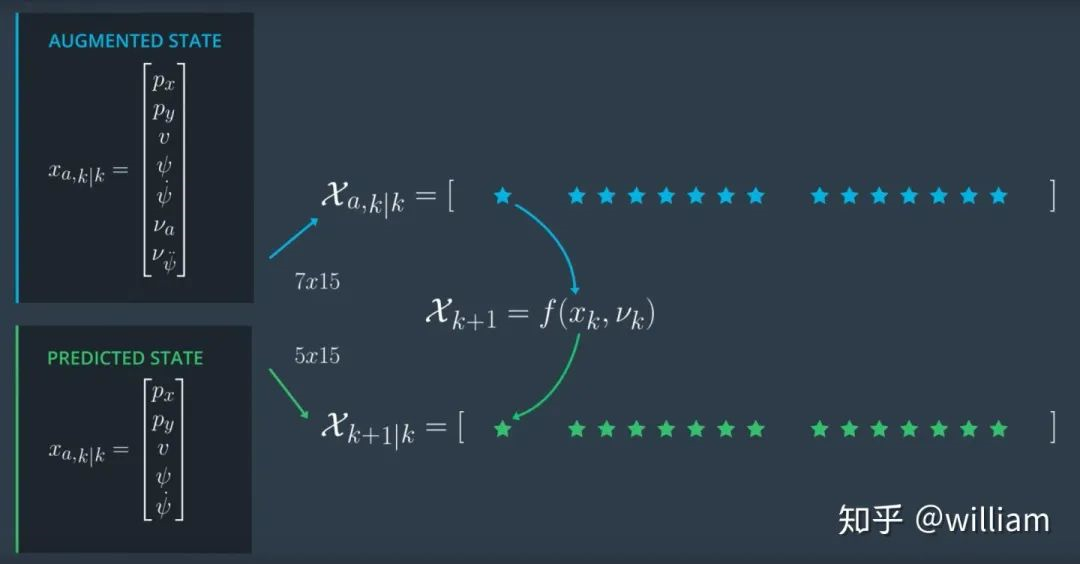
此处需要注意最初状态向量是5维,过程模型的输入是个7维增强向量,过程模型返回5维向量,也就是说预测的sigma点的矩阵有5行15列。
使用预测的sigma点近似高斯分布,并计算均值和协方差
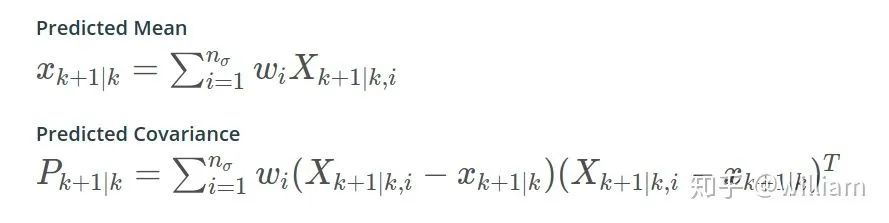
备注:对于权重公式,我在无迹转换参数中提到了一种详细的定义方式,此处使用简化的权重公式。除此之外有的人可能对于sigma点生成公式中出现扩散系数λ,而权重公式中又出现一次λ感到疑惑。这是因为我们在sigma点生成时,使用λ扩散sigma点,在我们预测了sigma点之后,如果我们需要恢复协方差矩阵,我们必须反转sigma点的扩散,这就是权重公式要做的事情,即协助重新近似新的高斯分布并计算其均值和协方差。
void UKF::Prediction(double delta_t) {
// create augmented mean vector
VectorXd x_aug = VectorXd(n_aug_);
// create augmented state covariance
MatrixXd P_aug = MatrixXd(n_aug_, n_aug_);
P_aug.fill(0.0);
// create sigma point matrix
MatrixXd Xsig_aug = MatrixXd(n_aug_, 2 * n_aug_ + 1);
Xsig_aug.fill(0.0);
// create augmented mean state
x_aug.head(n_x_) = x_;
x_aug(5) = 0;
x_aug(6) = 0;
// create augmented covariance matrix
P_aug.fill(0.0);
P_aug.topLeftCorner(n_x_, n_x_) = P_;
P_aug(5, 5) = std_a_ * std_a_;
P_aug(6, 6) = std_yawdd_ * std_yawdd_;
// create square root matrix
MatrixXd L = P_aug.llt().matrixL();
// create augmented sigma points
Xsig_aug.col(0) = x_aug;
for (int i = 0; i < n_aug_; ++i) {
Xsig_aug.col(i + 1) = x_aug + sqrt(lambda_ + n_aug_) * L.col(i);
Xsig_aug.col(i + 1 + n_aug_) = x_aug - sqrt(lambda_ + n_aug_) * L.col(i);
}
// predict sigma points
for (int i = 0; i < 2 * n_aug_ + 1; ++i) {
// extract values for better readability
double p_x = Xsig_aug(0, i);
double p_y = Xsig_aug(1, i);
double v = Xsig_aug(2, i);
double yaw = Xsig_aug(3, i);
double yawd = Xsig_aug(4, i);
double nu_a = Xsig_aug(5, i);
double nu_yawdd = Xsig_aug(6, i);
// predicted state values
double px_p, py_p;
// avoid division by zero
if (fabs(yawd) > 0.001) {
px_p = p_x + v / yawd * (sin(yaw + yawd * delta_t) - sin(yaw));
py_p = p_y + v / yawd * (cos(yaw) - cos(yaw + yawd * delta_t));
} else {
px_p = p_x + v * delta_t * cos(yaw);
py_p = p_y + v * delta_t * sin(yaw);
}
double v_p = v;
double yaw_p = yaw + yawd * delta_t;
double yawd_p = yawd;
// add noise
px_p = px_p + 0.5 * nu_a * delta_t * delta_t * cos(yaw);
py_p = py_p + 0.5 * nu_a * delta_t * delta_t * sin(yaw);
v_p = v_p + nu_a * delta_t;
yaw_p = yaw_p + 0.5 * nu_yawdd * delta_t * delta_t;
yawd_p = yawd_p + nu_yawdd * delta_t;
// write predicted sigma point into right column
Xsig_pred_(0, i) = px_p;
Xsig_pred_(1, i) = py_p;
Xsig_pred_(2, i) = v_p;
Xsig_pred_(3, i) = yaw_p;
Xsig_pred_(4, i) = yawd_p;
}
//create vector for predicted state
// create covariance matrix for prediction
x_.fill(0.0);
for (int i = 0; i < 2 * n_aug_ + 1; ++i) {
x_ = x_ + weights_(i) * Xsig_pred_.col(i);
}
P_.fill(0.0);
for (int i = 0; i < 2 * n_aug_ + 1; ++i) {
VectorXd x_diff = Xsig_pred_.col(i) - x_;
while (x_diff(3) > M_PI) x_diff(3) -= 2. * M_PI;
while (x_diff(3) < -M_PI) x_diff(3) += 2. * M_PI;
P_ = P_ + weights_(i) * x_diff * x_diff.transpose();
}
}
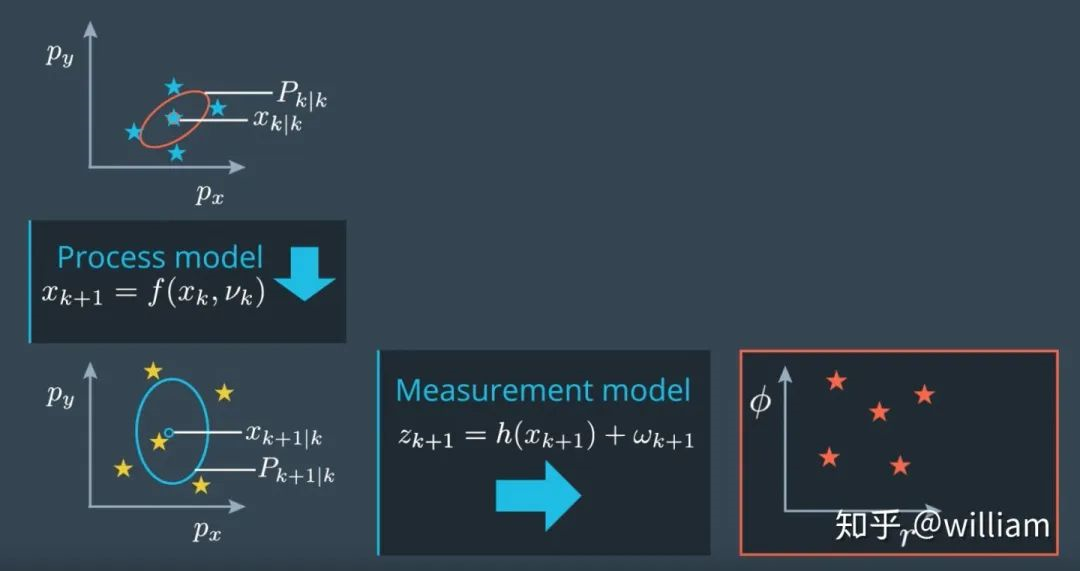
测量阶段
a. 雷达测量
由于预测状态空间到雷达测量空间是非线性变换,因此我们需要执行无迹变化,将sigma 点放入测量模型中。原本我们需要用之前得到的预测空间的高斯分布生成一遍sigma点,但是这里我们可以有两个捷径。
首先,我们可以将“预测步骤”已经生成的预测sigma 点直接放入测量模型中。
其次,我们不必使用测量噪声矢量来增强预测的sigma点,即在测量模型中,预测状态空间sigma 点的维度是5(之前在预测模型中增强状态是7),因为它在我们的测量模型中没有非线性影响。
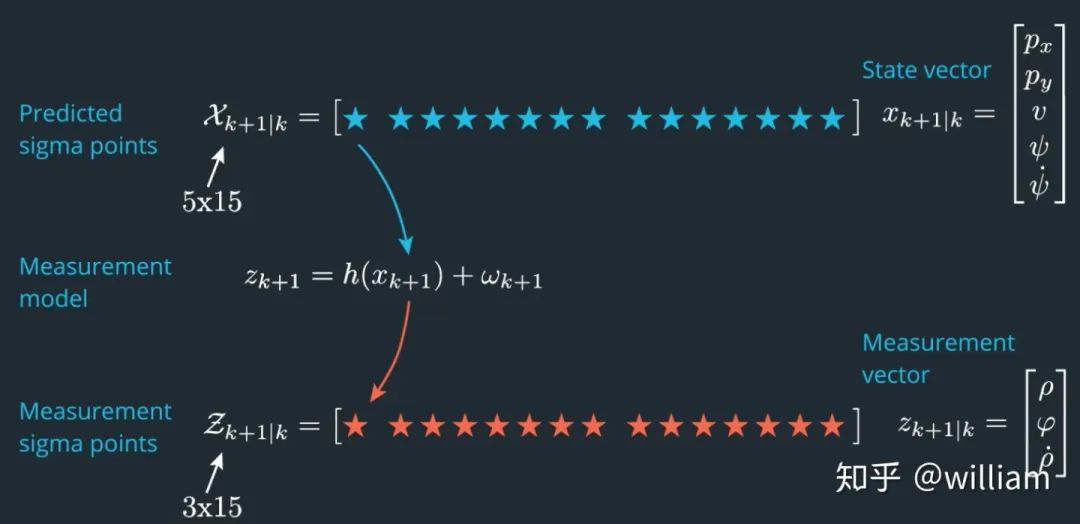

值得注意的是雷达测量更新,需要首先使用非线性转换函数h(x)将状态向量从预测空间转换到测量空间。

这里我们需要添加测量协方差噪声R, 值得注意的是ωk+1是单纯的误差累计,不具有非线性,其对测量预测结果的影响由R表示,因此在代码中,zk+1的推导没有ωk+1项,一般情况下测量协方差噪声R中各项的标准差会由硬件厂商给出。

void UKF::UpdateRadar(MeasurementPackage meas_package) {
// set measurement dimension, radar can measure r, phi, and r_dot
int n_z_ = 3;
VectorXd z = VectorXd(n_z_);
double meas_rho = meas_package.raw_measurements_(0);
double meas_phi = meas_package.raw_measurements_(1);
double meas_rhod = meas_package.raw_measurements_(2);
z << meas_rho,
meas_phi,
meas_rhod;
// create matrix for sigma points in measurement space
MatrixXd Zsig = MatrixXd(n_z_, 2 * n_aug_ + 1);
// mean predicted measurement
VectorXd z_pred = VectorXd(n_z_);
z_pred.fill(0.0);
// measurement covariance matrix S
MatrixXd S = MatrixXd(n_z_, n_z_);
S.fill(0.0);
// transform sigma points into measurement space
for (int i = 0; i < 2 * n_aug_ + 1; ++i) {
// 2n+1 simga points
// extract values for better readability
double p_x = Xsig_pred_(0, i);
double p_y = Xsig_pred_(1, i);
double v = Xsig_pred_(2, i);
double yaw = Xsig_pred_(3, i);
double v1 = cos(yaw) * v;
double v2 = sin(yaw) * v;
// measurement model
Zsig(0, i) = sqrt(p_x * p_x + p_y * p_y); //r
Zsig(1, i) = atan2(p_y, p_x); // phi
Zsig(2, i) = (p_x * v1 + p_y * v2) / sqrt(p_x * p_x + p_y * p_y); //r_dot
//calculate mean predicted measurement
z_pred += weights_(i) * Zsig.col(i);
}
///////////////////////////////////////////////////
// the above code is different for Radar and Lidar Measurement Update
// the following is just similiar
//////////////////////////////////////////////////
// innovation covariance matrix S
for (int i = 0; i < 2 * n_aug_ + 1; ++i) {
// 2n+1 simga points
// residual
VectorXd z_diff = Zsig.col(i) - z_pred;
// angle normalization
while (z_diff(1) > M_PI) z_diff(1) -= 2. * M_PI;
while (z_diff(1) < -M_PI) z_diff(1) += 2. * M_PI;
S += weights_(i) * z_diff * z_diff.transpose();
}
S += R_radar_;
// create matrix for cross correlation Tc
MatrixXd Tc = MatrixXd(n_x_, n_z_);
Tc.fill(0.0);
for (int i = 0; i < 2 * n_aug_ + 1; ++i) {
// 2n+1 simga points
// residual
VectorXd z_diff = Zsig.col(i) - z_pred;
// angle normalization
while (z_diff(1) > M_PI) z_diff(1) -= 2. * M_PI;
while (z_diff(1) < -M_PI) z_diff(1) += 2. * M_PI;
// state difference
VectorXd x_diff = Xsig_pred_.col(i) - x_;
// angle normalization
while (x_diff(3) > M_PI) x_diff(3) -= 2. * M_PI;
while (x_diff(3) < -M_PI) x_diff(3) += 2. * M_PI;
Tc += weights_(i) * x_diff * z_diff.transpose();
}
// Kalman gain K;
MatrixXd K = Tc * S.inverse();
// residual
VectorXd z_diff = z - z_pred;
// angle normalization
while (z_diff(1) > M_PI) z_diff(1) -= 2. * M_PI;
while (z_diff(1) < -M_PI) z_diff(1) += 2. * M_PI;
// update state mean and covariance matrix
x_ += K * z_diff;
P_ -= K * S * K.transpose();
// compute normalized innovation squared(NIS)
nis_radar_ = z_diff.transpose() * S.inverse() * z_diff;
}
b. 激光测量
激光测量更新的基本流程与雷达更新一致,唯一的区别在于不需要将转换预测状态空间到测量空间,即不需要非线性转换函数h(x),它们之间的传递是线性的。
void UKF::UpdateLidar(MeasurementPackage meas_package) {
// set measurement dimension, px,py
int n_z_ = 2;
// create example vector for incoming lidar measurement
VectorXd z = VectorXd(n_z_);
z << meas_package.raw_measurements_(0),
meas_package.raw_measurements_(1);
// create matrix for sigma points in measurement space
MatrixXd Zsig = MatrixXd(n_z_, 2 * n_aug_ + 1);
// mean predicted measurement
VectorXd z_pred = VectorXd(n_z_);
z_pred.fill(0.0);
// measurement covariance matrix S
MatrixXd S = MatrixXd(n_z_, n_z_);
S.fill(0.0);
// transform sigma points into measurement space
for (int i = 0; i < 2 * n_aug_ + 1; ++i) {
// 2n+1 simga points
// extract values for better readability
double p_x = Xsig_pred_(0, i);
double p_y = Xsig_pred_(1, i);
// measurement model
Zsig(0, i) = p_x;
Zsig(1, i) = p_y;
// mean predicted measurement
z_pred += weights_(i) * Zsig.col(i);
}
///////////////////////////////////////////////////
// the above code is different for Radar and Lidar Measurement Update
// the following is just similiar
//////////////////////////////////////////////////
// innovation covariance matrix S
for (int i = 0; i < 2 * n_aug_ + 1; ++i) {
// 2n+1 simga points
// residual
VectorXd z_diff = Zsig.col(i) - z_pred;
S += weights_(i) * z_diff * z_diff.transpose();
}
S += R_lidar_;
// create matrix for cross correlation Tc
MatrixXd Tc = MatrixXd(n_x_, n_z_);
Tc.fill(0.0);
for (int i = 0; i < 2 * n_aug_ + 1; ++i) {
// 2n+1 simga points
// residual
VectorXd z_diff = Zsig.col(i) - z_pred;
// state difference
VectorXd x_diff = Xsig_pred_.col(i) - x_;
// normalize angles
while (x_diff(3) > M_PI) x_diff(3) -= 2 * M_PI;
while (x_diff(3) < -M_PI) x_diff(3) += 2 * M_PI;
Tc += weights_(i) * x_diff * z_diff.transpose();
}
// Kalman gain K;
MatrixXd K = Tc * S.inverse();
// residual
VectorXd z_diff = z - z_pred;
// update state mean and covariance matrix
x_ += K * z_diff;
P_ -= K * S * K.transpose();
// compute normalized innovation squared(NIS)
nis_lidar_ = z_diff.transpose() * S.inverse() * z_diff;
}
}
3. 更新状态和协方差矩阵

至此我们已经完成了整个无迹卡尔曼滤波项目,实现了基于激光雷达和毫米波雷达的多目标追踪。
让我们来看看结果吧!
第一个项目是简单的对单一目标的追踪:
GITHUB代码库:github.com/williamhyin/

第二个项目稍微复杂点是对多目标的追踪:
GITHUB代码库: github.com/williamhyin/
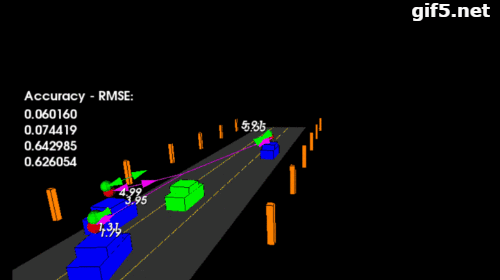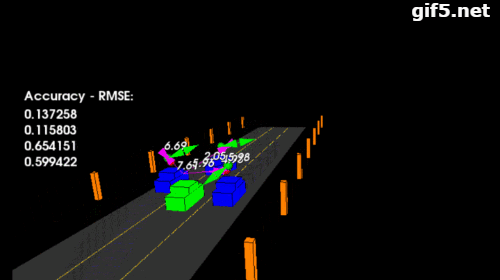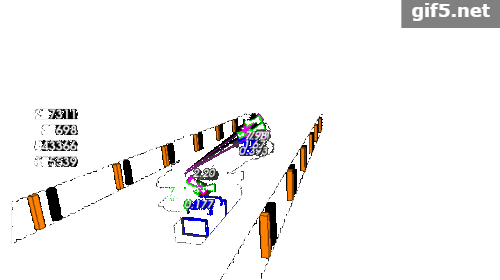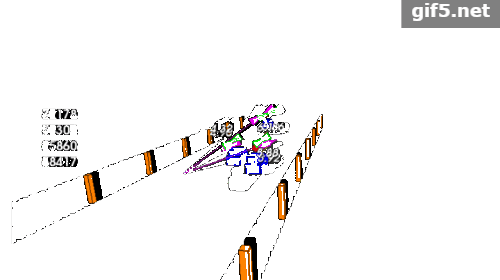
备注: 汽车上方的红色球体代表激光雷达探测的(x,y),紫色线条雷达探测到的沿着探测角度的速度大小。 在跟踪时没有考虑 z 轴,因此只沿 x / y 轴进行跟踪。而绿色球体上面的数字,箭头的长度和方向,代表经过无迹卡尔曼滤波预测后的车辆的位置(x,y),速度和角度。
如果有什么疑问,可以随时联系我的个人邮箱。
如果你觉得我的文章对你有帮助,请帮忙点个赞~\(≧▽≦)/~
- 用户评论