轩辕实验室┃一种应用于GPS反欺骗的基于MLE的RAIM改进方法
来源:
2021-03-16
2869
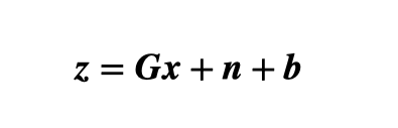
其中z是一个M维向量,表示伪距残差;G是从解空间到测量空间的M×4几何矩阵。x是一个二维矢量,包括时钟偏差和位置;n是一个M维向量,表示测量误差,每个元素服从标准差等于σ的独立零均值高斯分布;b是没有补偿的测量偏差(故障)的多维向量。在欺骗下,b代表欺骗偏差,其分量bi(1
基于最小二乘法,可以得到的估计量
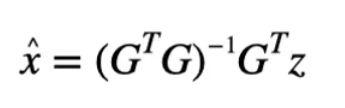
其等效于将M维的向量z投影到四维的解空间,这会导致信息丢失。因此,可以构造奇偶矩阵来恢复丢失的信息,该信息是M-4维的奇偶矢量。结果如下:
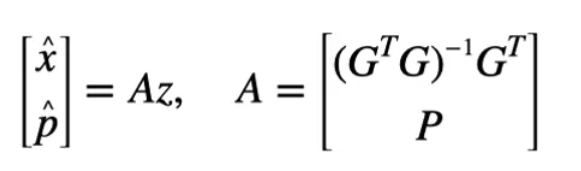
其中是奇偶矢量,P是(M-4)×M维的奇偶矩阵。而奇偶矢量可以由如下公式所求:
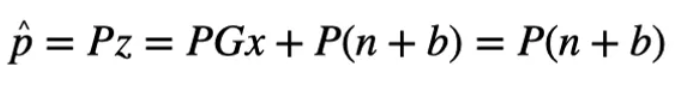
因此,可以获得奇偶矢量的数学期望和方差:
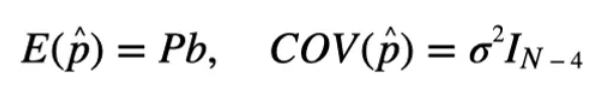
其中是(1≤i≤M)的方差,并且是ni的第i个分量。
因此,测得的伪距残差矢量w可以表示为
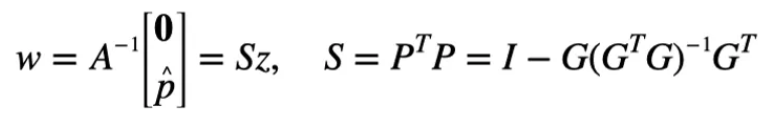
最后,获得误差平方和SSE:
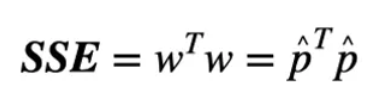
可以证明,当b = 0(无故障且无欺骗信号)时,SSE符合中心卡方分布;当b≠0时,SSE符合非中心卡方分布。卡方分布的自由度为M-4 。由于SSE的概率分布是已知的,因此可以通过预设的虚假警报概率来确定检测阈值Tsse
。例如,如果误报率为1‰,M等于10,则Tsse等于22.4577。
在五个以上的卫星信号且其中只有一个卫星故障的情况下,基于条件概率P(p|b)的最大值,常规RAIM也可以用于故障排除。具体描述如下
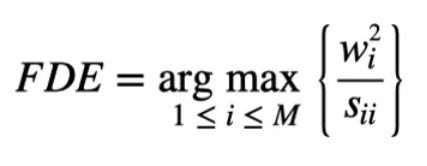
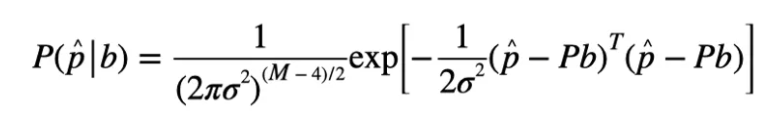
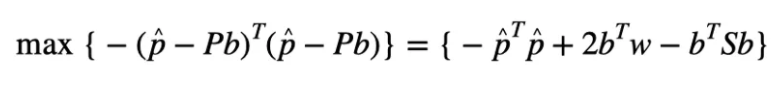
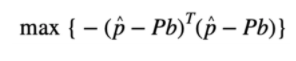
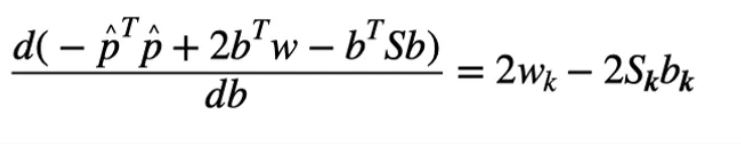
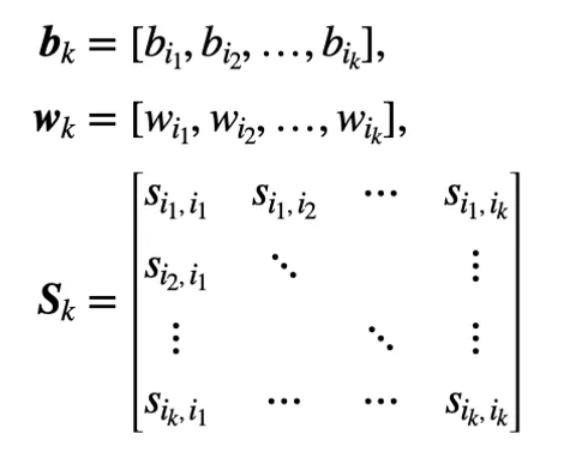
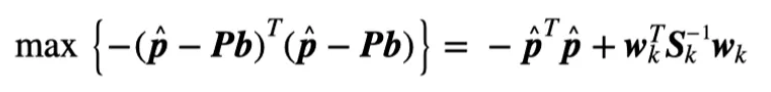
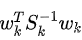 的最大值来获得对应的k个欺骗信号数FDEs:
的最大值来获得对应的k个欺骗信号数FDEs: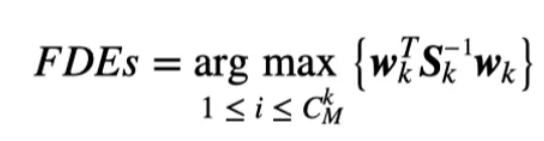
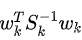 的值。可以通过比较所有值来获得最大值。根据MLE理论,对应于
的值。可以通过比较所有值来获得最大值。根据MLE理论,对应于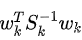 最大值的信号是欺骗信号。因此,在假设有k个欺骗信号的情况下,与需要大约次的随机遍历RAIM方法相比,通过执行一次常规RAIM可以找到对应的欺骗信号, 计算复杂度大大降低。
最大值的信号是欺骗信号。因此,在假设有k个欺骗信号的情况下,与需要大约次的随机遍历RAIM方法相比,通过执行一次常规RAIM可以找到对应的欺骗信号, 计算复杂度大大降低。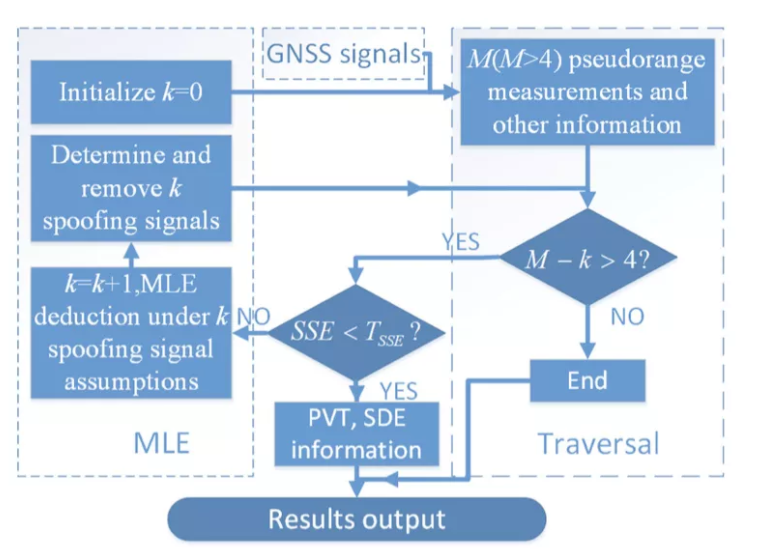
初始化k=0
根据伪距,卫星坐标和预设的误报率,计算SSE和
执行RAIM测试,比较SSE和 如果RAIM没有报错,输出正确的位置、速度、时间 如果RAIM报错了,使k=k+1;然后在有K个欺骗信号的假设下执行上述MLE推论。 找到使()最大的k个欺骗信号并移除这些信号;然后回到步骤2 当M-K小于等于4或RAIM测试没有报错时,循环终止


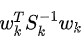 的最大值相对应的组合。在图中,红色括号中的坐标表示与120个统计量中的最大值相对应的坐标,其统计量在三个不同时间处最大的组合为组合3。因此,TMRAIM方法有效地找到了所有欺骗信号。
的最大值相对应的组合。在图中,红色括号中的坐标表示与120个统计量中的最大值相对应的坐标,其统计量在三个不同时间处最大的组合为组合3。因此,TMRAIM方法有效地找到了所有欺骗信号。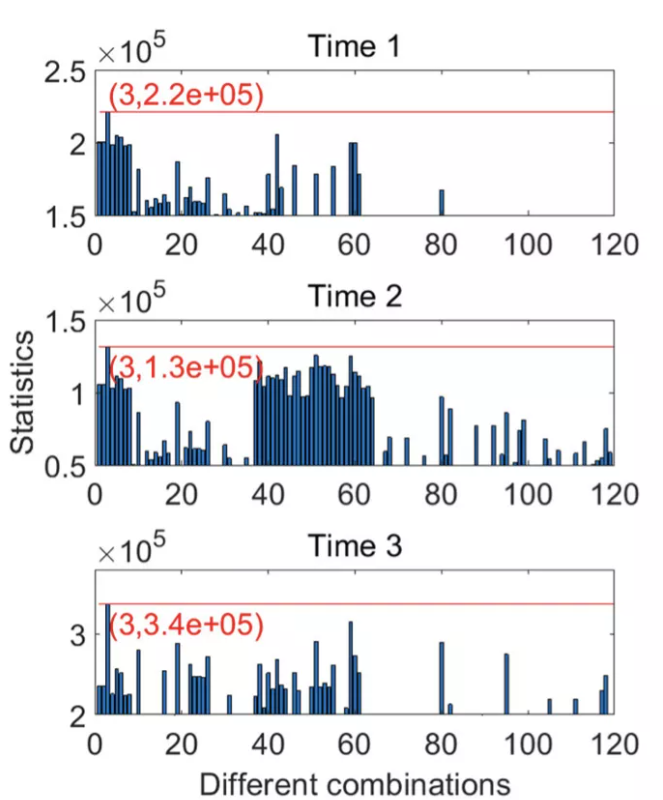

收藏
点赞
- 用户评论
2000
评论